491. 递增子序列

给你一个整数数组 nums ，找出并返回所有该数组中不同的递增子序列，递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。

数组中可能含有重复元素，如出现两个整数相等，也可以视作递增序列的一种特殊情况。

示例 1：

输入：nums = [4,6,7,7]
输出：[[4,6],[4,6,7],[4,6,7,7],[4,7],[4,7,7],[6,7],[6,7,7],[7,7]]

示例 2：

输入：nums = [4,4,3,2,1]
输出：[[4,4]]

提示：

• 1 <= nums.length <= 15
• -100 <= nums[i] <= 100

思路

这个递增子序列比较像是取有序的子集。而且本题也要求不能有相同的递增子序列。

这又是子集，又是去重，是不是不由自主的想起了刚刚讲过的回溯算法：求子集问题（二）。

就是因为太像了，更要注意差别所在，要不就掉坑里了！

在回溯算法：求子集问题（二）中我们是通过排序，再加一个标记数组来达到去重的目的。

而本题求自增子序列，是不能对原数组经行排序的，排完序的数组都是自增子序列了。

所以不能使用之前的去重逻辑！

本题给出的示例，还是一个有序数组 [4, 6, 7, 7]，这更容易误导大家按照排序的思路去做了。

为了有鲜明的对比，我用[4, 7, 6, 7]这个数组来举例，抽象为树形结构如图：

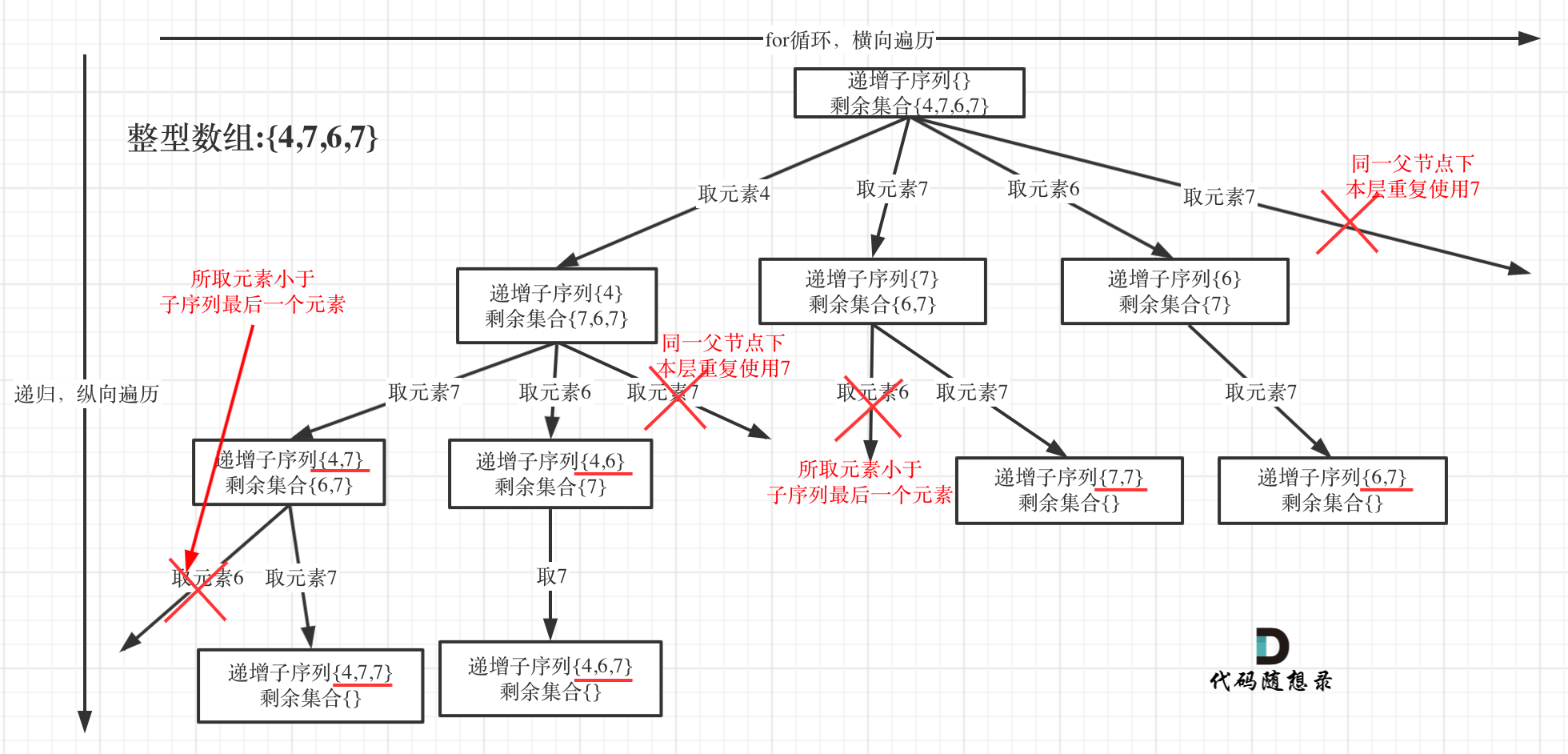
解法

class Solution {

    List<List<Integer>> result = new ArrayList<>();
    List<Integer> list = new ArrayList<>();

    public List<List<Integer>> findSubsequences(int[] nums) {
        if (nums == null || nums.length == 0) {
            return result;
        }
        backtracking(nums, 0);
        return result;
    }

    public void backtracking(int[] nums, int start) {
        if (list.size() > 1) {
            result.add(new ArrayList<>(list));
        }
        if (start == nums.length) {
            return;
        }
        Map<Integer, Integer> existMap = new HashMap<>();
        for (int i = start; i < nums.length; i++) {
            // 判断当前值之前是否已经使用过，不回溯
            if (i > 0 && existMap.containsKey(nums[i])) {
                continue;
            }
            existMap.put(nums[i], 1);
            if (list.size() == 0 || nums[i] >= list.get(list.size() - 1)) {
                list.add(nums[i]);
                backtracking(nums, i + 1);
                list.remove(list.size() - 1);
            }
        }
    }
}