377. 组合总和 Ⅳ

题目链接

给你一个由 不同 整数组成的数组 nums ，和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。

题目数据保证答案符合 32 位整数范围。

示例 1：

输入：nums = [1,2,3], target = 4
输出：7
解释：
所有可能的组合为：
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
请注意，顺序不同的序列被视作不同的组合。

示例 2：

输入：nums = [9], target = 3
输出：0

提示：

• 1 <= nums.length <= 200
• 1 <= nums[i] <= 1000
• nums 中的所有元素 互不相同
• 1 <= target <= 1000

进阶：如果给定的数组中含有负数会发生什么？问题会产生何种变化？如果允许负数出现，需要向题目中添加哪些限制条件？

解法

1. 递归

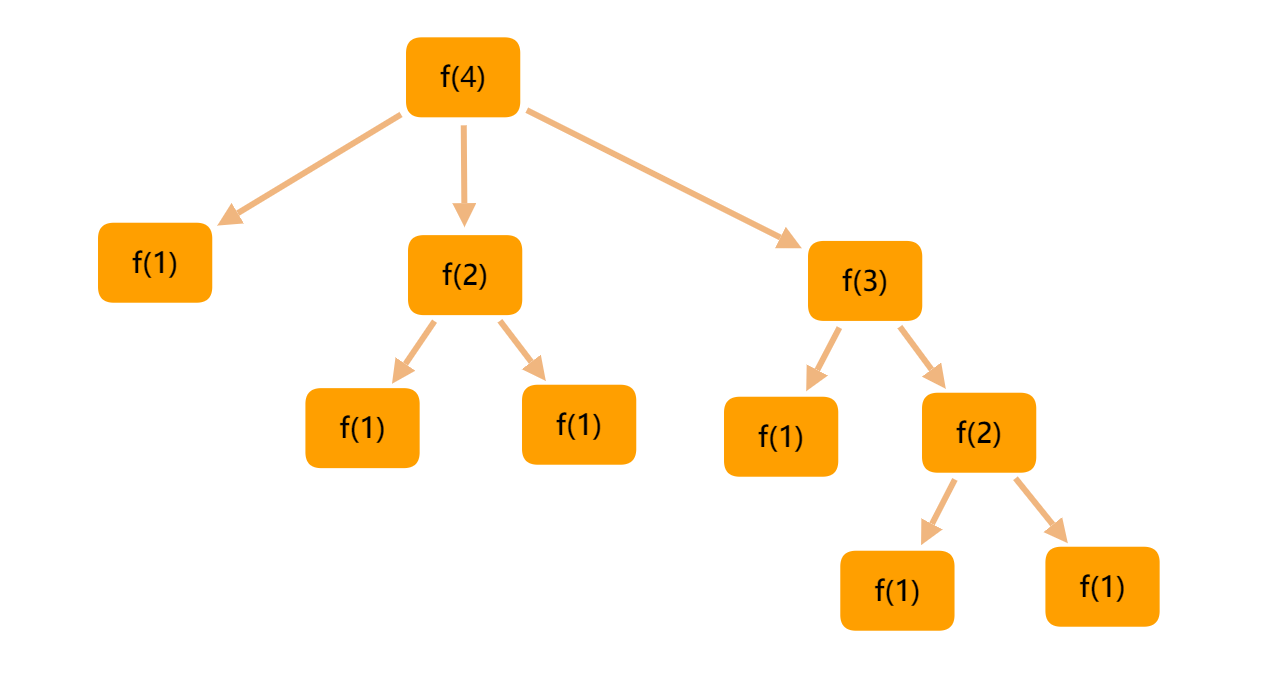
对于nums = [1,2,3], target = 4，假设

第一位选择 num[0] 时则有 f(4 - 1) = f(3) 种情况，

第一位选择 num[1] 时则有 f(4 - 2) = f[2) 中情况，

第一位选择 num[2] 时则有 f(4 - 3) = f(1) 中情况。

所以f(target) = f(target - num[0]) + f(target - num[1]) + ... + f(target - num[n - 1])

即： \(f[target] = \sum_{i=0}^{n - 1}{f[target - nums[i]]}\)

class Solution {
    public int combinationSum4(int[] nums, int target) {
        if (target == 0) {
            return 1;
        }
        if (target < 0) {
            return 0;
        }
        int res = 0;
        for (int i = 0; i < nums.length; i++) {
            res += combinationSum4(nums, target - nums[i]);
        }
        return res;
    }
}

递归效率较差，即使加上记忆化搜索在target比较大时还是会出现超时。

2. 动态规划

递归是自顶向下的，动态规划是自底向上的。递归时我们只关注 f(target - nums[i])有多少种情况即可，动态规划却需要从 f(0)开始一直迭代到 f(target)，所以设 dp[i]为 target为 i时的组合数量（是不是就是完全背包了），那么由于 \(f(target) = \sum_{i=0}^{n - 1}{f(target - nums[i])}\)，所以

\[\begin{align*} & dp[0] = f(0) = \sum_{i=0}^{n - 1}{f(0 - nums[i])},\\ & dp[1] = f(1) = \sum_{i=0}^{n - 1}{f(1 - nums[i])},\\ & \dots \\ & dp[target] = f(target) = \sum_{i=0}^{n - 1}{f(target - nums[i])} & \end{align*}\]

递归公式为完全背包的累加，只不过要先遍历 target 再遍历背包，和一般写法正好反过来。

但是 dp[0] 要初始化为 1，没有实际意义，只是计算需要。

class Solution {
    public int combinationSum4(int[] nums, int target) {
        if (target < 0) {
            return 0;
        }
        int res = 0;
        int[] dp = new int[target + 1];
        dp[0] = 1;
        for (int i = 0; i <= target; i++) {
            for (int j = 0; j < nums.length; j++) {
                if (i - nums[j] >= 0) {
                    dp[i] += dp[i - nums[j]];
                }
            }
        }
        return dp[target];
    }
}