337. 打家劫舍 III

题目链接

小偷又发现了一个新的可行窃的地区。这个地区只有一个入口，我们称之为 root 。

除了 root 之外，每栋房子有且只有一个“父“房子与之相连。一番侦察之后，聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ，房屋将自动报警。

给定二叉树的 root 。返回 在不触动警报的情况下 ，小偷能够盗取的最高金额。

示例 1:

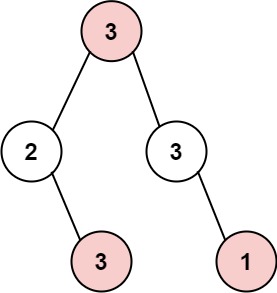
输入: root = [3,2,3,null,3,null,1]
输出: 7 
解释: 小偷一晚能够盗取的最高金额 3 + 3 + 1 = 7

示例 2:

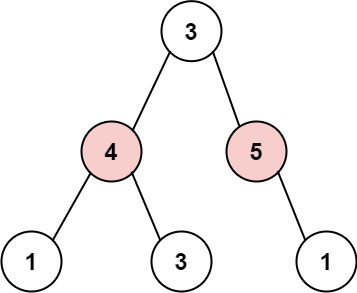
输入: root = [3,4,5,1,3,null,1]
输出: 9
解释: 小偷一晚能够盗取的最高金额 4 + 5 = 9

提示：

• 树的节点数在 [1, 104] 范围内
• 0 <= Node.val <= 104

解法

1. 递归遍历+记忆化搜索

树形递归，只需要比较偷父节点和不偷父节点两种情况下的最大值即可。

class Solution {
    Map<TreeNode, Integer> map = new HashMap<>();
    public int rob(TreeNode root) {
        if (root == null) {
            return 0;
        }
        if (map.containsKey(root)) {
            return map.get(root);
        }
        // 不偷父节点
        int m = rob(root.left) + rob(root.right);
        // 偷父节点
        int n = root.val;
        if (root.left != null) {
            n += rob(root.left.left) + rob(root.left.right);
        }
        if (root.right != null) {
            n += rob(root.right.left) + rob(root.right.right);
        }
        int max = Math.max(m, n);
        map.put(root, max);
        return max;
    }
}

2. 树形DP

上面的方法，其实对一个节点偷与不偷得到的最大金钱都没有做记录，而是需要实时计算。

而动态规划其实就是使用状态转移容器来记录状态的变化，这里可以使用一个长度为 2 的数组，记录当前节点偷与不偷所得到的的最大金钱。

class Solution {
    public int rob(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int[] res = search(root);
        return Math.max(res[0], res[1]);
    }

    /**
     * 树形 DP
     * @param root 当前节点
     * @return int[0]: 偷当前节点的结果，int[1]: 不偷当前节点的结果
     */
    public int[] search(TreeNode root) {
        if (root == null) {
            return new int[]{0, 0};
        }
        int[] left = search(root.left);
        int[] right = search(root.right);
        int[] res = new int[2];
        res[0] = root.val + left[1] + right[1];
        // 如果不偷当前节点，那么左右孩子就可以偷，注意此时 left 和 right 数组表示的是偷不偷 left 和 right 节点的结果，而不是偷不偷当前节点的结果
        res[1] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
        return res;
    }
}