114. 二叉树展开为链表

题目链接

给你二叉树的根结点 root ，请你将它展开为一个单链表：

• 展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
• 展开后的单链表应该与二叉树 先序遍历 顺序相同。

示例 1：

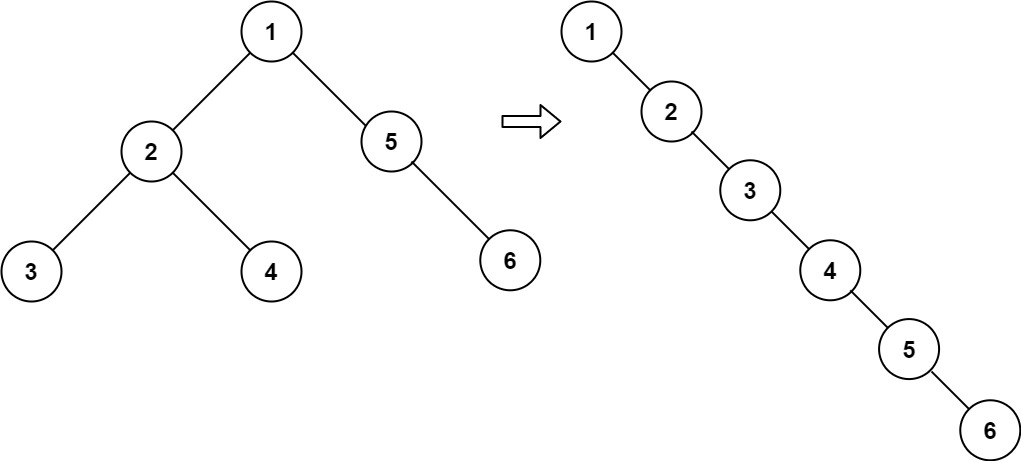
输入：root = [1,2,5,3,4,null,6]
输出：[1,null,2,null,3,null,4,null,5,null,6]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [0]
输出：[0]

提示：

• 树中结点数在范围 [0, 2000] 内
• -100 <= Node.val <= 100

进阶：你可以使用原地算法（O(1) 额外空间）展开这棵树吗？

解法

1. 递归

把原二叉树改造为链表其实就是改造成一个只有单边的树，所有可以把一个节点的左右子树分开，左子树连接到父节点的右边，原右子树连接到原左子树后面，如下示例：

    1
   / \
  2   5
 / \   \
3   4   6

//将 1 的左子树插入到右子树的地方
    1
     \
      2         5
     / \         \
    3   4         6        
//将原来的右子树接到左子树的最右边节点
    1
     \
      2          
     / \          
    3   4  
         \
          5
           \
            6
            
 //将 2 的左子树插入到右子树的地方
    1
     \
      2          
       \          
        3       4  
                 \
                  5
                   \
                    6   
        
 //将原来的右子树接到左子树的最右边节点
    1
     \
      2          
       \          
        3      
         \
          4  
           \
            5
             \
              6         

2 递归

    1
   / \
  2   5
 / \   \
3   4   6

题目其实就是将二叉树通过右指针，组成一个链表。

题目要求先序遍历的顺序，所以我们能不能利用先序遍历的代码，每遍历一个节点，就将上一个节点的右指针更新为当前节点。

先序遍历的顺序是 1 2 3 4 5 6。

遍历到 2，把 1 的右指针指向 2。1 -> 2 3 4 5 6。

遍历到 3，把 2 的右指针指向 3。1 -> 2 -> 3 4 5 6。

… …

一直进行下去似乎就解决了这个问题。但现实是残酷的，原因就是我们把 1 的右指针指向 2，那么 1 的原本的右孩子就丢失了，也就是 5 就找不到了。

解决方法的话，我们可以逆过来进行。

我们依次遍历 6 5 4 3 2 1，然后每遍历一个节点就将当前节点的右指针更新为上一个节点。

遍历到 5，把 5 的右指针指向 6。6 <- 5 4 3 2 1。

遍历到 4，把 4 的右指针指向 5。6 <- 5 <- 4 3 2 1。

… …

    1
   / \
  2   5
 / \   \
3   4   6

代码如下：

class Solution {
    TreeNode pre = null;
    public void flatten(TreeNode root) {
        if (root == null) {
            return;
        }
        flatten(root.right);
        flatten(root.left);
        root.right = pre;
        root.left = null;
        pre = root;
    }
}

3 迭代

迭代前序遍历，可以避免递归时修改导致节点无法遍历的问题。

class Solution {
    public void flatten(TreeNode root) {
        if (root == null) {
            return;
        }
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        TreeNode pre = null;
        TreeNode cur = null;
        while (!stack.isEmpty()) {
            cur = stack.pop();
            if (pre != null) {
                pre.right = cur;
                pre.left = null;
            }
            if (cur.right != null) {
                stack.push(cur.right);
            }
            if (cur.left != null) {
                stack.push(cur.left);
            }
            pre = cur;  
        }
    }
}