111. 二叉树的最小深度

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

示例 1：

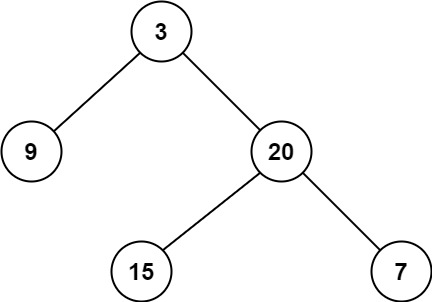
输入：root = [3,9,20,null,null,15,7]
输出：2

示例 2：

输入：root = [2,null,3,null,4,null,5,null,6]
输出：5

提示：

• 树中节点数的范围在 [0, 105] 内
• -1000 <= Node.val <= 1000

思路

BFS遍历，遇到叶子节点则终止并返回当前深度。

递归思路个陷阱。

解法

1. 迭代

class Solution {
    public int minDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        ArrayDeque<TreeNode> deque = new ArrayDeque<>();
        deque.offer(root);
        int depth = 0;
        int levelSize = 0;
        while (!deque.isEmpty()) {
            levelSize = deque.size();
            depth++;
            while (!deque.isEmpty() && levelSize > 0) {
                root = deque.poll();
                //叶子节点
                if (root.left == null && root.right == null) {
                    return depth;
                }
                if (root.left != null) {
                    deque.offer(root.left);
                }
                if (root.right != null) {
                    deque.offer(root.right);
                }
                levelSize--;
            }
        }
        return depth;
    }
}

2. 递归

这块和104题求最大深度可就不一样了，一些同学可能会写如下代码：

int leftDepth = getDepth(node.left);
int rightDepth = getDepth(node.right);
int result = 1 + Math.min(leftDepth, rightDepth);
return result;

这个代码就犯了此图中的误区：

如果这么求的话，没有左孩子的分支会算为最短深度。

所以，如果左子树为空，右子树不为空，说明最小深度是 1 + 右子树的深度。

反之，右子树为空，左子树不为空，最小深度是 1 + 左子树的深度。 最后如果左右子树都不为空，返回左右子树深度最小值 + 1 。

class Solution {
    public int minDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int leftDepth = minDepth(root.left);
        int rightDepth = minDepth(root.right);
        if (root.left != null && root.right == null) {
            return leftDepth + 1;
        }
        if (root.left == null && root.right != null) {
            return rightDepth + 1;
        }
        return Math.min(leftDepth, rightDepth) + 1;
    }
}