106. 从中序与后序遍历序列构造二叉树

根据一棵树的中序遍历与后序遍历构造二叉树。

注意: 你可以假设树中没有重复的元素。

例如，给出

中序遍历 inorder = [9,3,15,20,7]
后序遍历 postorder = [9,15,7,20,3]

返回如下的二叉树：

    3
   / \
  9  20
    /  \
   15   7

思路

二叉树问题递归解决。问题是后序遍历和中序遍历有什么规律？

后续遍历的最后一个元素是根节点，通过根节点在中序遍历中的位置从而可以知道其左右两棵子树的位置和节点数量，那么根据左子树的节点数量可以知道其在后续数组中的位置，而左右两棵子树又可以递归看作两棵二叉树，获取最后一个节点就是子树的根节点，如此递归即可求出所有节点的左右子节点。递归的终止条件就是节点为叶子节点或者节点为null。

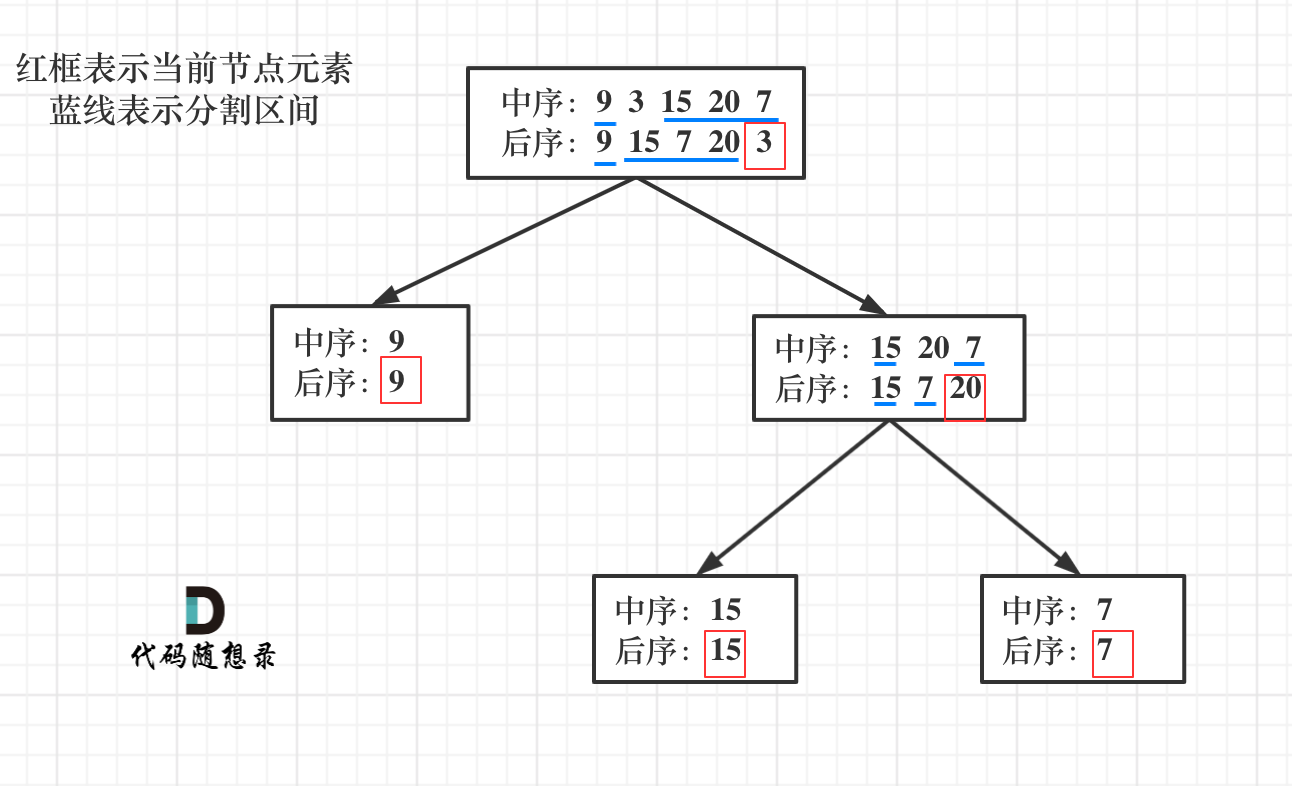
解法

class Solution {
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        if (postorder.length == 1) {
            return new TreeNode(postorder[0]);
        }
        return build(inorder, 0, inorder.length - 1, postorder, 0, postorder.length - 1);
    }

    public TreeNode build(int[] inorder, int inLeft, int inRight, int[] postorder, int postLeft, int postRight) {
        if (inLeft > inRight) {
            return null;
        }
        if (inLeft == inRight) {
            return new TreeNode(inorder[inLeft]);
        }
        
        //获取当前根节点
        TreeNode root = new TreeNode(postorder[postRight]);
        //获取根节点在前序数组中的位置，从而可以知道其左右两棵子树的大小
        int inSeparator = getInorderSeparatorPos(inorder, root.val);
        
        //获取左右子树在后续数组中的分隔位置（左子树节点数量为inSeparator - inLeft）
        int postSeparator = postLeft + inSeparator - inLeft - 1;
        
        //递归求左子节点
        TreeNode leftNode = build(inorder, inLeft, inSeparator - 1, postorder, postLeft, postSeparator);
        //递归求右子节点
        TreeNode rightNode = build(inorder, inSeparator + 1, inRight, postorder, postSeparator + 1, postRight - 1);

        root.left = leftNode;
        root.right = rightNode;
        return root;
    }
    
    /**
     * 获取根节点在中序数组中的位置
     */
    public int getInorderSeparatorPos(int[] inorder, int val) {
        for (int i = 0; i < inorder.length; i++) {
            if (inorder[i] == val) {
                return i;
            }
        }
        return 0;
    }
}