98. 验证二叉搜索树

给定一个二叉树，判断其是否是一个有效的二叉搜索树。

假设一个二叉搜索树具有如下特征：

• 节点的左子树只包含小于当前节点的数。
• 节点的右子树只包含大于当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

示例 1:

输入:
    2
   / \
  1   3
输出: true

示例 2:

输入:
    5
   / \
  1   4
     / \
    3   6
输出: false
解释: 输入为: [5,1,4,null,null,3,6]。
     根节点的值为 5 ，但是其右子节点值为 4 。

思路

由于中序遍历顺序为 左-中-右，所以二叉树的中序遍历一定为升序。可以在中序遍历的时候维护一个前值或者把中序遍历结果保存进数组，判断数组升序即可。

如果递归判断根节点比左子树所有节点值大，比右节点所有节点值小也是可以的。

递归过程存在两个陷阱一定要注意：

1. 不能单纯的比较左节点小于中间节点，右节点大于中间节点就完事了。

   所以要比较的是左子树的最大值和右子树的最小值

   

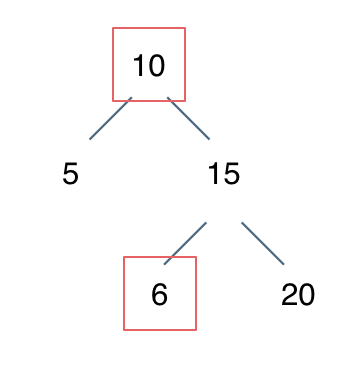
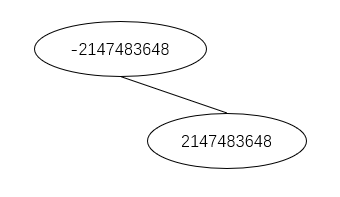
2. 样例中最小节点 可能是int的最小值，如果这样使用最小的int来比较也是不行的。

   题目中的数值类型是 int 型，所以接收的时候可以使用 long

   

解法

1. 中序遍历升序

class Solution {
    //如果声明的是数值的话要使用 Long.MIN_VALUE;
    public TreeNode preNode;
    public boolean isValidBST(TreeNode root) {
        if (root == null) {
            return true;
        }
        return inOrderTraversalCheck(root);
    }

    public boolean inOrderTraversalCheck(TreeNode root) {
        if (root == null) {
            return true;
        }
        boolean leftFlag = inOrderTraversalCheck(root.left);
        if (!leftFlag) {
            return false;
        }
        //判断是否递增
        if (preNode != null && root.val <= preNode.val) {
            return false;
        }
        preNode = root;
        return inOrderTraversalCheck(root.right);
    }
}

2. 递归判断

遍历过程维护左子树最大值和右子树最小值。

class Solution {
    public boolean isValidBST(TreeNode root) {
        if (root == null) {
            return true;
        }
        return check(root).isValidBST;
    }

    public ValidBST check(TreeNode root) {
        if (root == null) {
            return new ValidBST(true);
        }
        
        ValidBST leftValid = check(root.left);
        ValidBST rightValid = check(root.right);
        
        if (!(leftValid.isValidBST && rightValid.isValidBST)) {
            return new ValidBST(false);
        }
        //左子树最大值
        if (leftValid.max != null && leftValid.max.val >= root.val) {
            return new ValidBST(false);
        }
        //右子树最小值
        if (rightValid.min != null && rightValid.min.val <= root.val) {
            return new ValidBST(false);
        }
        //维护当前树最大值和最小值节点
        TreeNode min = leftValid.min == null ? root : leftValid.min;
        TreeNode max = rightValid.max == null ? root : rightValid.max;
        return new ValidBST(min, max, true);
    }

    static class ValidBST {
        //当前树最小值
        TreeNode min;
        //当前树最大值
        TreeNode max;
        //当前树是否为BST
        boolean isValidBST;

        public ValidBST(boolean isValidBST) {
            this.isValidBST = isValidBST;
        }

        public ValidBST(TreeNode min, TreeNode max, boolean isValidBST) {
            this.min = min;
            this.max = max;
            this.isValidBST = isValidBST;
        }
    }
}