85. 最大矩形

题目

题目链接

给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

示例 1：

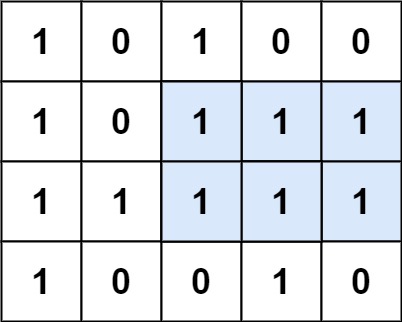
输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：6
解释：最大矩形如上图所示。

示例 2：

输入：matrix = []
输出：0

示例 3：

输入：matrix = [["0"]]
输出：0

示例 4：

输入：matrix = [["1"]]
输出：1

示例 5：

输入：matrix = [["0","0"]]
输出：0

提示：

• rows == matrix.length
• cols == matrix[0].length
• 1 <= row, cols <= 200
• matrix[i][j] 为 '0' 或 '1'

解法

利用单调栈。竖直方向遇 1 累加，遇 0 置为 0，可以计算出每个位置竖直方向的矩形面积。

水平方向这时候利用 84 题思路即可以求出这几个竖直矩形所组成的最大矩形面积。

public static int maximalRectangle(char[][] matrix) {
    if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
        return 0;
    }
    char[] data = matrix[0];
    int maxArea = 0;
    maxArea = Math.max(maxArea, findMax(data));

    for (int i = 1; i < matrix.length; i++) {
        //竖直方向遇 1 累加，遇  0置为 0，求出竖直方向矩形高度
        for (int j = 0; j < matrix[i].length; j++) {
            data[j] = matrix[i][j] == '0' ? '0' : ++data[j];
        }
        maxArea = Math.max(maxArea, findMax(data));
    }
    return maxArea;
}

/**
 * 利用单调栈求出每一行为底，当前所有矩形所组成的最大矩形面积
 */
public static int findMax(char[] row) {
    Stack<Integer> stack = new Stack<>();
    int i = 0;
    int maxArea = 0;
    int width = 0;
    while (i < row.length) {
        while (!stack.isEmpty() && row[i] < row[stack.peek()]) {
            int pop = stack.pop();
            width = i - (stack.isEmpty() ? -1 : stack.peek()) - 1;
            maxArea = Math.max(maxArea, (row[pop] - '0') * width);
        }
        stack.push(i++);
    }

    int right = stack.isEmpty() ? 0 : stack.peek();
    while (!stack.isEmpty()) {
        int pop = stack.pop();
        width = right - (stack.isEmpty() ? -1 : stack.peek());
        maxArea = Math.max(maxArea, (row[pop] - '0') * width);
    }
    return maxArea;
}