84. 柱状图中最大的矩形

题目

题目链接

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1:

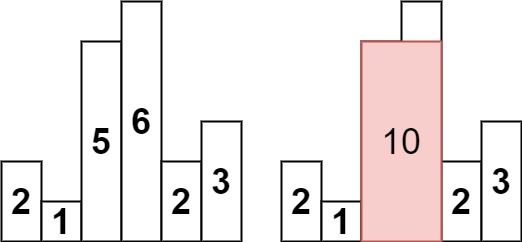
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

示例 2：

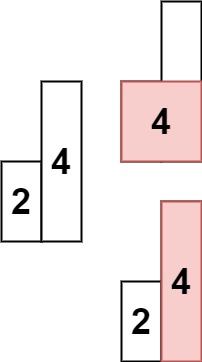
输入： heights = [2,4]
输出： 4

提示：

• 1 <= heights.length <=105
• 0 <= heights[i] <= 104

解法

依次遍历柱形的高度，对于每一个高度分别向两边扩散，求出以当前高度为矩形的最大宽度多少。

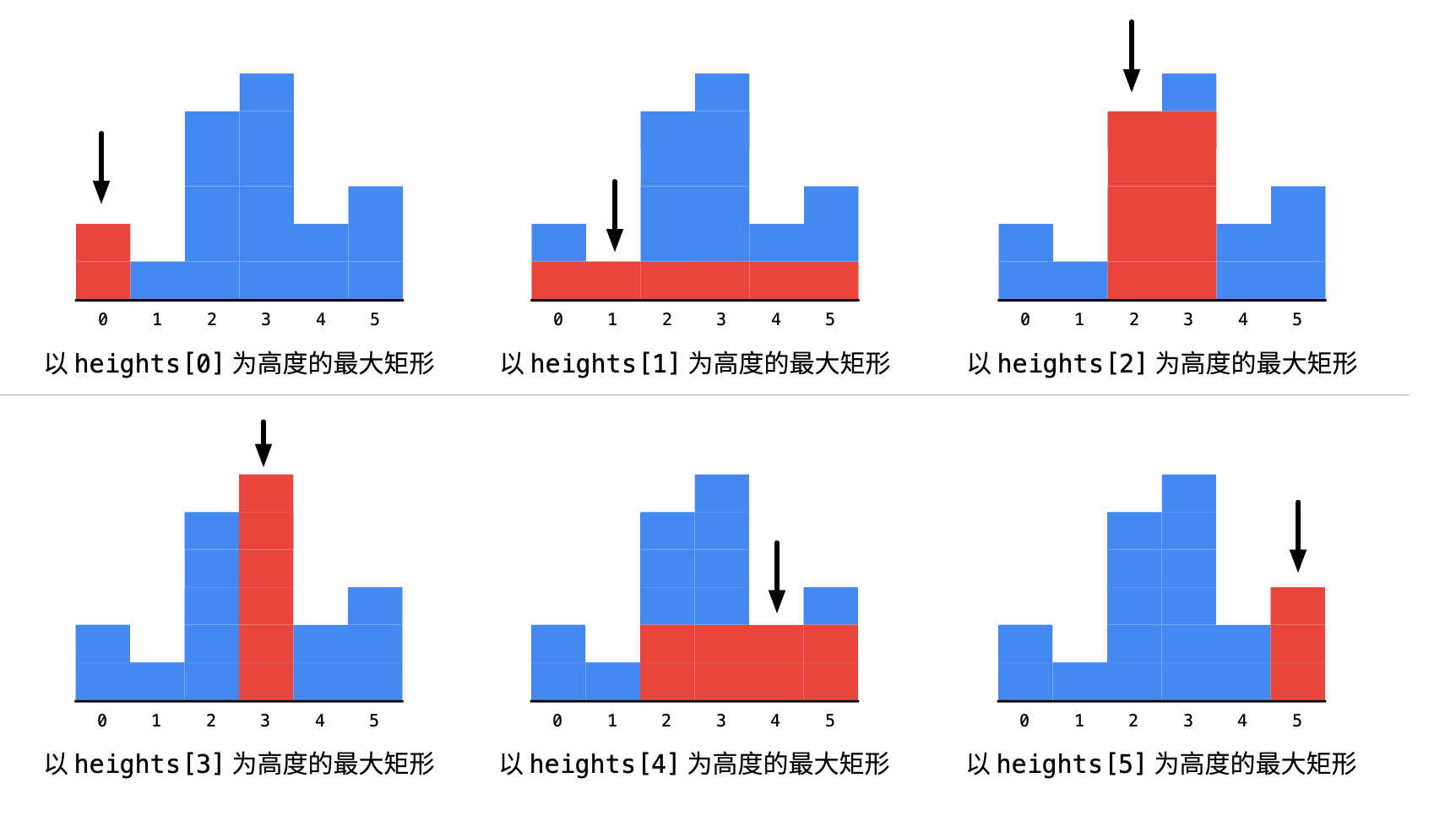
1 暴力破解

以每个柱子为中心向两边遍历直到找到比自己矮的柱子停止，可以得到以当前柱子高度所能形成的最大矩形面积。

2 单调栈

核心逻辑就是找到每一根柱子两边比自己矮的柱子。

而单调递增栈则正好满足这个条件。单调栈的写法为：

// 遍历数组
for (int i = 0; i < nums. length; i++) {
    // 栈不为空 && 栈顶元素小于当前元素
    while (!stack.isEmpty() && stack.peek() < nums[i]) {
        // 栈顶元素出栈
        stack.pop();
    }
    // 当前数据入栈
    stack.push(nums[i]);
}

栈顶元素当做目标高度的柱子，那么栈顶的第二个元素就是左边比自己矮的第一根柱子，而待入栈的元素就是右边比自己矮的第一根柱子。所以利用栈顶和栈顶的下一个元素以及要入栈的元素，这三个元素正好就能确定以当前栈顶元素为高度标准的向左右两边扩展所能得到的最大矩形。代码为：

class Solution {
    public int largestRectangleArea(int[] heights) {
        // 因为要寻找向左和向右扩散的右边界，即左右两边比自己矮的柱子，所以使用单调递减栈
        Stack<Integer> stack = new Stack<>();
        int maxArea = 0;
        int width;
        int curArea;
        for (int i = 0; i < heights.length; i++) {
            // 栈不为空 && 栈顶元素小于当前元素
            while (!stack.isEmpty() && heights[stack.peek()] > heights[i]) {
                // 栈顶元素出栈
                int curIndex = stack.pop();
                // 以当前元素为高度向左扩散的边界为此时栈顶的元素，右边界为此时待入栈的元素
                width = i - (stack.isEmpty() ? -1 : stack.peek()) - 1;
                curArea = width * heights[curIndex];
                maxArea = Math.max(maxArea, curArea);
            }
            // 当前数据入栈
            stack.push(i);
        }

        // 此时还在栈中的元素的右边界全部为此时栈顶元素或数组的右边界
        int right = stack.isEmpty() ? -1 : stack.peek();
        while (!stack.isEmpty()) {
            // 栈顶元素出栈
            int curIndex = stack.pop();
            // 以当前元素为高度向左扩散的边界为此时栈顶的元素
            width = right - (stack.isEmpty() ? -1 : stack.peek());
            curArea = width * heights[curIndex];
            maxArea = Math.max(maxArea, curArea);
        }
        return maxArea;
    }
}