15. 三数之和

给你一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？请你找出所有和为 0 且不重复的三元组。

注意：答案中不可以包含重复的三元组。

示例 1：

输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]

示例 2：

输入：nums = []
输出：[]

示例 3：

输入：nums = [0]
输出：[]

提示：

• 0 <= nums.length <= 3000
• -105 <= nums[i] <= 105

思路

之前做过 1. 两数之和，使用Map判断另一个值是否存在，3Sum 依然可以借助这个思路，先两两求和，再借助Map判断第三个元素是否存在。但是题目中要求“不重复的三元组”，因此需要进行去重，而这一步比较麻烦。

尝试使用双指针的话，我一开始是想先排序，left 指针指向 num[0]，right 指针指向 nums[nums.length - 1]，然后判断两者之和是否大于 0，如果大于 0，mid 指针从 left + 1 位置开始向右移动，如果小于 0 则从 right - 1 位置开始向左移动，直到三者和为 0 或者 mid 与 right/left 指针相遇。不知道有没有人也有这种想法。这种方法存在的问题就是当前循环结束后下一轮循环需要判断两种情况，比如：当前为（nums[0]、nums[nums.length - 1]），下一轮就要同时判断（nums[1]、nums[nums.length - 1]）和（nums[0]、nums[nums.length - 2]）。

双指针

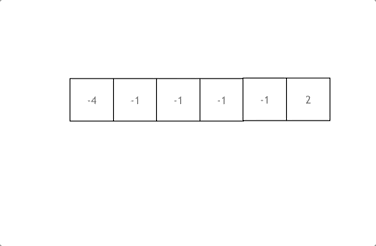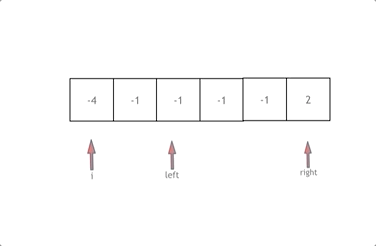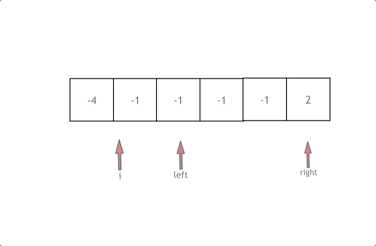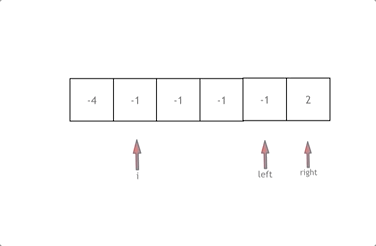
思路如上图：先排序，然后从左到右一次剪枝数组。设 a = num[i]，那么只需要在剩余数组中找到 b、c 使得 a + b + c = 0 即可，设 left 指向剩余数组的左边界，right 指向剩余数组的右边界，那么只要 num[i] + num[left] + num[right] = 0 即可。如果 num[i] + num[left] + num[right] > 0，因为数组是排序的，所以只需要 right 指针右移即可，如果 num[i] + num[left] + num[right] < 0，那么只需要 left 指针左移即可。

public List<List<Integer>> threeSum(int[] nums) {
    List<List<Integer>> result = new ArrayList<>();
    if (nums.length < 3) {
        return result;
    }
    Arrays.sort(nums);

    int left = 0;
    int right = 0;
    int sum = 0;
    
    // 剩余数组数据量不能小于3
    for (int i = 0; i < nums.length - 2; i++) {
        // 最小值大于0，后续都不用计算
        if (nums[i] > 0) {
            return result;
        }
        
        if (i > 0 && nums[i] == nums[i - 1]) {
            // 利用 for 循环右移
            continue;
        }
        
        left = i + 1;
        right = nums.length - 1;

        while (left < right) {
            sum = nums[left] + nums[right] + nums[i];
            if (sum == 0) {
                if (left > i + 1 && nums[left] == nums[left - 1]) {
                    left++;
                    continue;
                }
                if (right < nums.length - 1 && nums[right] == nums[right + 1]) {
                    right--;
                    continue;
                }
                result.add(Arrays.asList(nums[i], nums[left], nums[right]));
                // 左右指针同时向内移动，不然会陷入死循环
                left++;
                right--;
            } else if (sum < 0) {
                left++;
            } else {
                right--;
            }
        }
    }
    return result;
}